• 一、实验综述
• 二、实验原理
  - 1.Gabor特征
  - 2.PCA
  - 3.线性回归的分类器
• 三、实验步骤
  - 1. 预处理
  - 2 特征提取
  - 3. 预测分类
  - 4. 参数调整
• 四、 实验结果
  - 实验结果讨论 ：
  - 参考文献
  - 实验代码

一、实验综述

人脸数据集中，共有16个人，每人至少有五幅图像，要求选取 5 幅图像，其中四幅图作为训练集，剩下一副图作为测试集。要求利用训练集训练模型，从测试集任选一幅图像，能够识别他的身份。

本文思路如下：首先对图像进行预处理，利用最近邻算法重采样规整为 128*128的灰度图像，并对亮度异常的图像进行调整。然后利用Gabor滤波器对灰度图像进行五尺度，八个方向的特征提取。接着利用PCA算法对图像数据进行压缩，选取贡献率前95%的特征向量作为新的基。最后分类算法采取线性回归的分类器，预测测试集中图像所属类别，并得到识别率。为了探讨不同Gabor滤波器的参数对识别结果的影响，选取了多组参数进行参数敏感性分析。

二、实验原理

1.Gabor特征

Gabor变换属于加窗傅立叶变换，Gabor函数可以在频域不同尺度、不同方向上提取相关的特征。【1】Gabor小波与人类视觉系统中简单细胞的视觉刺激响应非常相似。它在提取目标的局部空间和频率域信息方面具有良好的特性。Gabor小波对于图像的边缘敏感，能够提供良好的方向选择和尺度选择特性，而且对于光照变化不敏感,能够提供对光照变化良好的适应性。上述特点使Gabor小波被广泛应用于视觉信息理解。
通过频率参数和高斯函数参数的选取，Gabor变换可以选取很多纹理特征，但是Gabor是非正交的，不同特征分量之间有冗余。 Gabor是有高斯核函数与复正弦函数调制而成，如下图所示。

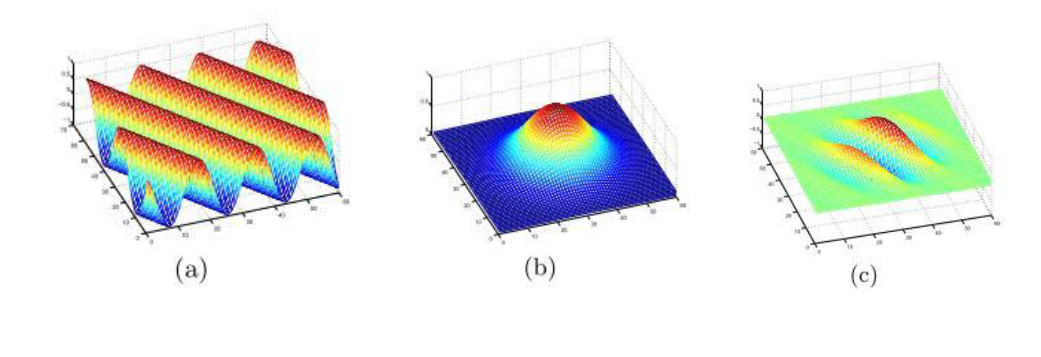
图(a)为偏移x轴30°的正弦函数，图(b)为高斯核，图©为对应的Gabor filter。可以看出正弦函数是如何在空间上具有局部性的。

2.PCA

PCA的原理就是将原来的样本数据投影到一个新的空间中，相当于我们在矩阵分析里面学习的将一组矩阵映射到另外的坐标系下。通过一个转换坐标，也可以理解成把一组坐标转换到另外一组坐标系下，但是在新的坐标系下，表示原来的原本不需要那么多的变量，只需要原来样本的最大的一个线性无关组的特征值对应的空间的坐标即可。

3.线性回归的分类器

线性子空间思想：一副人脸图像可由本类人脸图像线性表示。

​ y=X_i*β_i=x_i1*β_i1+x_i2*β_i2+⋯+x_im*β_im

其中，y为测试图像，
X_i=[x_i1,…,x_im ]为第 i 类训练,i=1,…,c,β_i=[β_i1,…,β_im ] 为表示系数。

然后利用最小二乘法求解〖 β〗_i 。证明如下：
可以写出最小二乘问题的矩阵形式：
∃B∉〖R(A)〗^ ,B∈R_n,min┬(X∈R^2 )⁡ ∥AX-B∥_2^

易知使得距离最小的向量 X 与使得距离平方最小的向量 X 是相同的，于是我们可以将所求的目标改写为：
min┬(X∈R^2 )⁡ ∥AX-B∥_2^2
而
∥AX-B∥_2^2=(AX-B)^T (AX-B)^
对原式化简并求其对 X 的导数:
(∂∥AX-B∥_2^2)/∂x=2A^T AX-2A^T b=0
得到最小二乘法的矩阵形式：
X=(A^T A)^(-1) A^T B
然后计算测试图像到第 i 类的距离：测试图像在第i类的表示误差。
d_i=||y-X_i (β_i ) ̂||^2
ID= min┬i⁡〖d_i 〗
即属于第 i 类

三、实验步骤

1. 预处理

​ 由于图像各异，预处理是人脸识别过程中的一个重要环节。输入图像由于图像采集环境的不同，如光照明暗程度以及设备性能的优劣等，往往存在有噪声，对比度不够等缺点。另外，距离远近，焦距大小等又使得人脸在整幅图像中间的大小和位置不确定。为了保证人脸图像中人脸大小，位置以及人脸图像质量的一致性，必须对图像进行预处理。
人脸图像的预处理主要包括人脸扶正，人脸图像的增强，以及归一化等工作。人脸扶正是为了得到人脸位置端正的人脸图像；图像增强是为了改善人脸图像的质量，不仅在视觉上更加清晰图像，而且使图像更利于计算机的处理与识别。归一化工作的目标是取得尺寸一致，灰度取值范围相同的标准化人脸图像。下面简单介绍一些预处理的方法。

​ 对于人脸扶正，采用matlab 内置函数ginput,手动点击人的两眼以及嘴唇，然后自动裁切为128*128的灰度图像

​ 有些照片曝光过度，或者光源不足，便对其进行处理，利用imadjust，对其进行亮度调杰。使图像的细节更加清楚，以减弱光线和光照强度的影响。
最后imreshape 对图像矩阵进行变形压缩，imwrite 使图像保存为bmp格式。

2 特征提取

对图像提取Gabor特征，尺度维数为5,角度维数为8,使其成为(6553601)的一维列向量
计算64张图片的均值，对数据矩阵（65536064）减去均值，然后计算协方差矩阵。
因为此协方差矩阵维数（655360*655360）过大，若直接计算，会引发out of memory ,采用一个小技巧。

假设 x 为 m×n 的矩阵, m≫n,S=x*x^’,PCA需要计算 S 最大的 k 个特征值以及对应的特征向量。但是m×m维度太大，无法直接求解。

令 C = x^'x ,CV=aV, a 为特征值，V为特征向量，xCV=xx^'xV=axV, S(xV)=a*(xV).

所以假设 a 是 C 的特征值，那么(a,xV) 是S的特征值和特征向量。如此可以化简计算过程
然后计算 每幅图在 协方差矩阵贡献率前95%的特征向量所构成的基上的投影。

3. 预测分类

根据线性分类器的阐述，计算其所在分类

4. 参数调整

根据实验结果，修改Gabor尺度和位置参数，寻求最佳参数。

四、 实验结果

        实验一   实验二	实验三	     实验四
准确率	0.3750	 0.4500	  0.5631	 0.7000

其中实验一为，不对图像进行任何处理，仅转为128128的bmp图像，然后进行实验。
实验二为，对图像进行裁切操作，转为128128的bmp图像,使图像主体为面部，且对图像进行亮度调节。
实验三为，对图像进行裁切，且对图像进行亮度调节，利用Gabor小波提取五尺度八方向特征，在不同参数，不同测试集下的平均准确率
实验四 对图像进行裁切，且对图像进行亮度调节，利用Gabor小波提取五尺度八方向特征，其中尺度、方向特征选取为学习得到的最优参数。
除实验三外，其余实验均为16个测试集得到的一次准确率。

将20个人分为20个类别，可以准确预测15个人的身份，其中第5个人预测失败，准确率达到 70.00%

实验结果讨论 ：

1.利用PCA可以对数据进行降维压缩，便于之后的操作处理
2.原图中有许多噪音或与人脸特征无关的背景、灯光等，对图像进行处理后，识别准确率得到提升。
3.若直接运用PCA算法进行识别，可以推出，此算法对人脸的方向、光照的强度、人脸侧面或是正面具有较强的敏感性，而Gabor特征只能解决光照敏感性、以及图像方向性这两个问题。对实验结果可知，识别失败的人脸类别主要为在训练集或训练集中出现侧脸拍照的情况。若改进这个问题，人脸识别的准确率将会得到进一步的提升。如何改进这个问题，则是实验可以进一步完善的地方

参考文献

1、《数字图像处理与matlab 实现》，电子工业出版社，杨杰

2、《数字图像处理》，冈萨雷兹

3、《基于PCA‐SIFT 算法的人脸识别技术的研究》

4、如何理解Gabor滤波器 | Wenyuan

实验代码

function pic_first
close all
n=80;
%% 从图像中扣取人脸
for i= 6
 path=strcat('D:\学习资料\成电\课\水课\矩阵分析\人脸识别作业\Test\Bmp\',int2str(i),'_nearest.bmp');
 img=imread(path);

 imshow(img)
 [x,y] = ginput(3);   
% 1 left eye, 2 right eye, 3 top of nose

cos = (x(2)-x(1))/sqrt((x(2)-x(1))^2+(y(2)-y(1))^2);
sin = (y(2)-y(1))/sqrt((x(2)-x(1))^2+(y(2)-y(1))^2);
mid_x = round((x(1)+x(2))/2);
mid_y = round((y(2)+y(1))/2);
d = round(sqrt((x(2)-x(1))^2+(y(2)-y(1))^2));
rotation = atan(sin./cos)*180/pi;
img = imrotate(img,rotation,'bilinear','crop'); 
figure(3), imshow(img);%人脸校正

[h,w] = size(img);
leftpad = mid_x-d;
if leftpad<1
   leftpad = 1;
end
toppad =mid_y - round(1.25*d);
if toppad<1
   toppad = 1;
 end
 rightpad = mid_x + d;
 if rightpad>w
    rightpad = w;
 end
 bottompad = mid_y + round(2*d);
 if bottompad>h
    bottompad = h;
 end   
 I1 =[];
 I2 =[];
 I1(:,:) = img(toppad:bottompad,leftpad:rightpad);
 I2(:,:) = imresize(I1,[128 128]); 
 I2=uint8(I2);
 figure,imshow(uint8(I2));
 name=strcat('D:\学习资料\成电\课\水课\矩阵分析\人脸识别作业\Test\Bmp\',int2str(i),'_nearest');
 imwrite(I2,strcat(name,'.bmp'));
end
%% 图像增强

for i=[2 6 9 13 14]
     path=strcat('D:\学习资料\成电\课\水课\矩阵分析\人脸识别作业\Test\Bmp\',int2str(i),'_nearest.bmp');
     img=imread(path); 
     imshow(img)
     Idouble = double(img); 
  	 mi = min(min(Idouble));
     ma=max(max(Idouble));
     J=imadjust(img);
	figure
    imshow(J)
    name=strcat('D:\学习资料\成电\课\水课\矩阵分析\人脸识别作业\Test\Bmp\',int2str(i),'_nearest');
    imwrite(J,strcat(name,'.bmp')); 
end

 
 %人脸裁剪

% 1 选取数据作为数据矩阵 size=128*128 
function [corre]=picture_gabor_pca(len,theta)
close all;
n=80;  % pic number
%  Gabor 特征
X=zeros(128*128*5*8,n);
%最优参数
% theta=[90   115   141   167   192   218   244   270];
%  len=[3 5 7 9 11]
for i=1:n
    path=strcat('D:\学习资料\成电\课\水课\矩阵分析\人脸识别作业\Train\Bmp\',int2str(i),'_nearest.bmp');
    m=imread(path);
    gaborArray = gabor(len,theta);
    gabormag=imgaborfilt(m,gaborArray);
    X(:,i)=gabormag(:);
end




% 2.均值向量 中心化， 协方差 绘制GABOR 变换图
mu=mean(X,2);
matrix=X-mu;
%%绘制Gabor特征图
% figure
% subplot(8,5,1);
% tt=128*128;
% for p = 1:40
%     subplot(8,5,p)
%     begin=tt*(p-1)+1;en=tt*p;
%     picu=uint8(X(begin:en));
%     picu=reshape(picu,[128 128]);
%     imshow(picu);
% %     theta = gaborArray(p).Orientation;
% %     lambda = gaborArray(p).Wavelength;
% %     title(sprintf('%d theta , %d len ',theta,lambda));
% end


% 3. Mat前K大特征值 特征向量 e,w = {eeee}   Trick c
S=matrix'*matrix; %
[vector values]=eig(S);% S的特征向量 特征值
Rvector=matrix*vector; % 协方差矩阵matrix*matrix'的特征向量

% Rvector values
Rvalues=diag(values);
[Rvalues  v_index]=sort(Rvalues,'descend');
Rvector=Rvector(:,v_index);

for j=1:length(Rvalues)
    if sum(Rvalues(1:j))/sum(Rvalues) >0.95
        Value=Rvalues(1:j);
        break;
    end
end
% 选取前K个向量
k=length(Value);
W=Rvector(:,1:k);

% 4 计算 每幅图像投影


Y=W'*matrix;
% 前k个特征脸
% for i=1:j
%     q=W(:,i);
% q=reshape(q,[128 128]);
% figure
% imshow(uint8(q));
% end

 


% 5.1 待识别人脸  图像识别率
data=zeros(n/4,3);
% an=zeros(n/4,n/4);
a=zeros(n/4,n/4);
for it=1:n/4
	 beta=zeros(4,n/4);
 	 an=zeros(1,n/4);
	 pre='D:\学习资料\成电\课\水课\矩阵分析\人脸识别作业\Test\Bmp\';suff='_nearest.bmp';
	 path=strcat(pre,int2str(it),suff);
	 m=imread(path);
	 gaborArray = gabor(len,theta);
	 gabormag=imgaborfilt(m,gaborArray);
	 z=gabormag(:);
	 z=double(z(:));
 	 z=W'*(z-mu);
	for i=1:n/4
   		 tem=Y(:,4*i-3:4*i);
   		 beta(:,i)=(tem'*tem)\tem'*z; 
		 a(it,i)=norm(z-tem*beta(:,i))^2;
   		 an(i)=norm(z-tem*beta(:,i))^2;
end
 	[sor index]=min(an);
	data(it,:)=[it index sor/10e20];
end

ze=find(data(:,1)==data(:,2));  
length(ze)
data(ze,:)
corre=length(ze)*4/n